Fig 1. The Clifton Suspension Bridge, Bristol, UK.

Now that we have an understanding of the fundamentals of dynamic behaviour for SDoF systems, we'll take what we've learned and generalise it for use with other types of dynamic loading. So far, we have explored harmonic loading (sine or cosine forcing functions). In reality we may need to analyse much more complex dynamic loading; perhaps the loading is not harmonic, or even periodic.

It may be the case that the loading was recorded experimentally e.g. wind speed data. There are many practical scenarios where a more versatile method of dynamic analysis is required. However, as you will see in this section we can actually make use of what we've already learned to perform this analysis.

There are a number of analysis procedures that can be employed to analyse complex non-harmonic loading for example Fourier decomposition mentioned earlier or the Duhamel integral approach. However, both of these methods require the use of superposition. As such, they are not applicable in cases where non-linear structural behaviour is expected.

A good example of non-linear structural behaviour is the behaviour of structures designed to survive an earthquake. Structures designed to resist collapse in the event of an earthquake are required to exhibit significant non-linear plastic behaviour. As such, dynamic analysis methods that assume linear structural behaviour are not appropriate.

Superposition methods are also not appropriate in cases where feedback exists between the applied load and structural response. One classic example of this is human-structure interaction (HSI). HSI, although rare, can be seen for example on bridges (mainly footbridges) and describes the phenomenon whereby the gait of members of the occupying crowd is altered in response to bridge motion. If this gait alteration leads to an increase in force magnitude or shift in frequency of force exciting the bridge, a positive feedback loop may be established. The London Millennium Footbridge and Clifton Suspension Bridge in Bristol are two such bridges that have exhibited this behaviour.

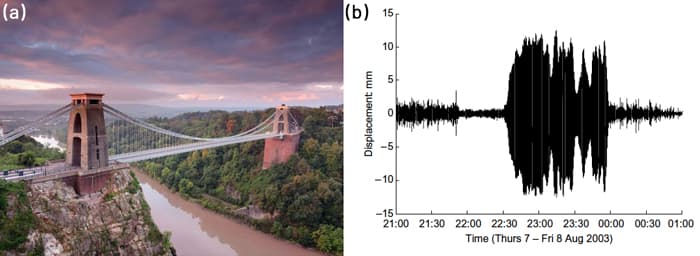
Fig 2. (a) Clifton Suspension Bridge (b) Lateral displacement of bridge deck observed during a crowd loading event

The image above (right) shows the recorded lateral vibration response on the Clifton Suspension Bridge during an event when the bridge was densely loaded with pedestrians. The large response increase was observed, when the crowd started to walk off the bridge. Clearly there was a form of feedback established between the crowd and bridge response that led to this uncharacteristic non-linear behaviour. Further details can be found in the referenced paper which is well worth reading (see the link in the lecture resource panel above).

Over the remaining lectures in this course we will introduce a method of analysis that does not require linear structural behaviour and that can accommodate feedback between loading and response. This method is general enough to be applied to any form of structural loading. Furthermore it is well suited to implementation within an algorithm, i.e. you can quite easily implement an algorithm to process loading data and evaluate structural response. The method we will explore is referred to as a step-by-step method.

This step-by-step method involve breaking the applied loading into a series of short duration segments and considering the response of the structure over each segment or time-step. The position and velocity of the structure at the end of one time-step become the initial position and velocity of the structure at the beginning of the next time-step. In this way the behaviour of the structure is determined step-by-step as the result of a succession of short duration linear analyses. We'll explore this concept in more detail in the next lecture.