In this lecture, we'll consider what happens when we apply the load quickly. Let's consider the same cantilever, except this time the load is applied rapidly with . Notice the different structural response, Fig 1.

Fig 1. Loading history indicating a rapidly applied load (top) and dynamic response of the free end of the cantilever (bottom).
Inertia
The load applied in Fig 1. above is applied dynamically (quickly) and as a result, we observe a dynamic structural response. This response is the result of inertia and to understand what's happening we need to understand what exactly inertia is and how we model it.
Put simply, inertia is a bodies resistance to a change in its velocity. This resistance can be modelled with an inertia force that is proportional to the mass and rate of change of velocity (acceleration). To illustrate inertia, consider a simple ball with mass in a state of static equilibrium on a frictionless surface, Fig. 2.
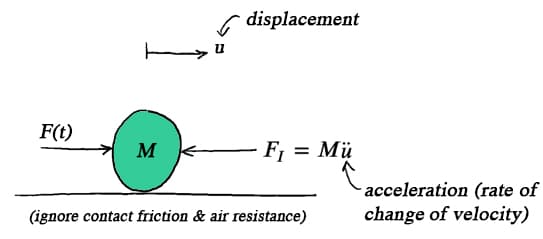
Fig 2. A ball with mass experiencing an externally applied force, . Inertia of the mass is modelled as an inertia force resisting a change in velocity of the mass.
Now consider the following:
-
If I want to change the velocity of the mass, , this will give rise to an acceleration (rate of change of velocity). Therefore there will be an inertia force I must overcome if I want to change the velocity of the ball. Remember, Newton tells us that all mass wants to resist a change in its velocity.
-
Once the ball is moving, if I remove the external force, , the ball will stay moving with a constant velocity (Newton 1). Therefore the inertia force disappears because there is no change in the velocity of the ball. Note that we're ignoring the influence of air resistance and friction that would naturally reduce the velocity of the ball.
-
When the velocity of the ball is constant, it is in a state of dynamic equilibrium. Newton 1 tells us that a mass always wants to maintain equilibrium (static or dynamic). This tendency of a mass to maintain dynamic equilibrium (i.e. resist changes in its velocity) can be modelled by applying an inertia force.
It's important to recognise that the inertia force is fictitious. It is not an externally applied force in the same way that is. Rather, it models the inherent behaviour of the mass, i.e. it models the masses resistance to a change in its own velocity.
Inertia summary
-
All mass resists changes in its velocity - mass wants to maintain equilibrium, if it's stationary, it wants to stay that way (static equilibrium), if it's moving, then it wants to maintain a constant velocity (dynamic equilibrium).
-
We can model this physical behaviour in our free-body diagrams and equations by applying a fictitious inertia force (known as D'Alembert's Principle).
-
The inertia force, is proportional to the mass , and the rate of change of velocity (acceleration), ,
Now that we understand inertia, we'll consider its influence on the behaviour of our cantilever beam in the next lecture.