Reinforced Concrete Column Design to ACI 318-14 with Python and concreteproperties

In this tutorial, we will cover the basics as well as explain some of the nuances of column design per ACI 318-14. This discussion focuses on non-sway, short columns. Extending the principles to sway or slender columns is, in my opinion, not difficult once the foundational concepts are understood, which this discussion includes in detail.

Although calculating column capacities is not difficult, it can be time-consuming to do by hand due to the number of intermediate calculations required.

concreteproperties by Robbie van Leeuwen

Thus, we will lean on programming to do the heavy lifting. This tutorial will feature concreteproperties, an open source Python package by Robbie van Leeuwen, which enables section property calculations, facilitating the analysis of reinforced concrete sections under combined axial and flexural loading.

Though not intended as a full substitute to commercial software, I find publicly available packages and libraries to be convenient and fast, particularly for quick design inspections and sanity checks.

1.0 What is a column?

A column is an axial-flexural member, similar to a beam, but primarily subjected to axial compression. Unlike beams, which experience mostly bending due to transverse loads, columns carry axial forces that can induce second-order moments due to $P-\Delta$ effects.

Generically speaking, in a gravity system, beams and slabs carry transverse (gravity) loads, which get transferred to the columns. The columns then transfer their loads down to the building's foundation, completing the load path.

In a lateral system, beams and columns work together as a moment frame to resist lateral forces. Typically, diaphragms (e.g. slabs) receive externally applied lateral loads. The diaphragm forces are distributed to the beams, causing bending in both the beam and column (with moments distributed based on their relative stiffnesses). These bending moments and axial forces propagate down to the foundation, completing the load path.

In an academic setting, columns are often introduced first as pinned-pinned, i.e. it is assumed that the column is a pure axial member, resisting no bending moments. While columns certainly are primarily axially loaded members, there are often non-negligible moments that must be accounted for in concrete column design. This is simply due to the nature of concrete as a material and reinforcement layouts that make it difficult to justify a truly pinned member. Let's take a closer look at the effects of gravity and lateral loads on a building.

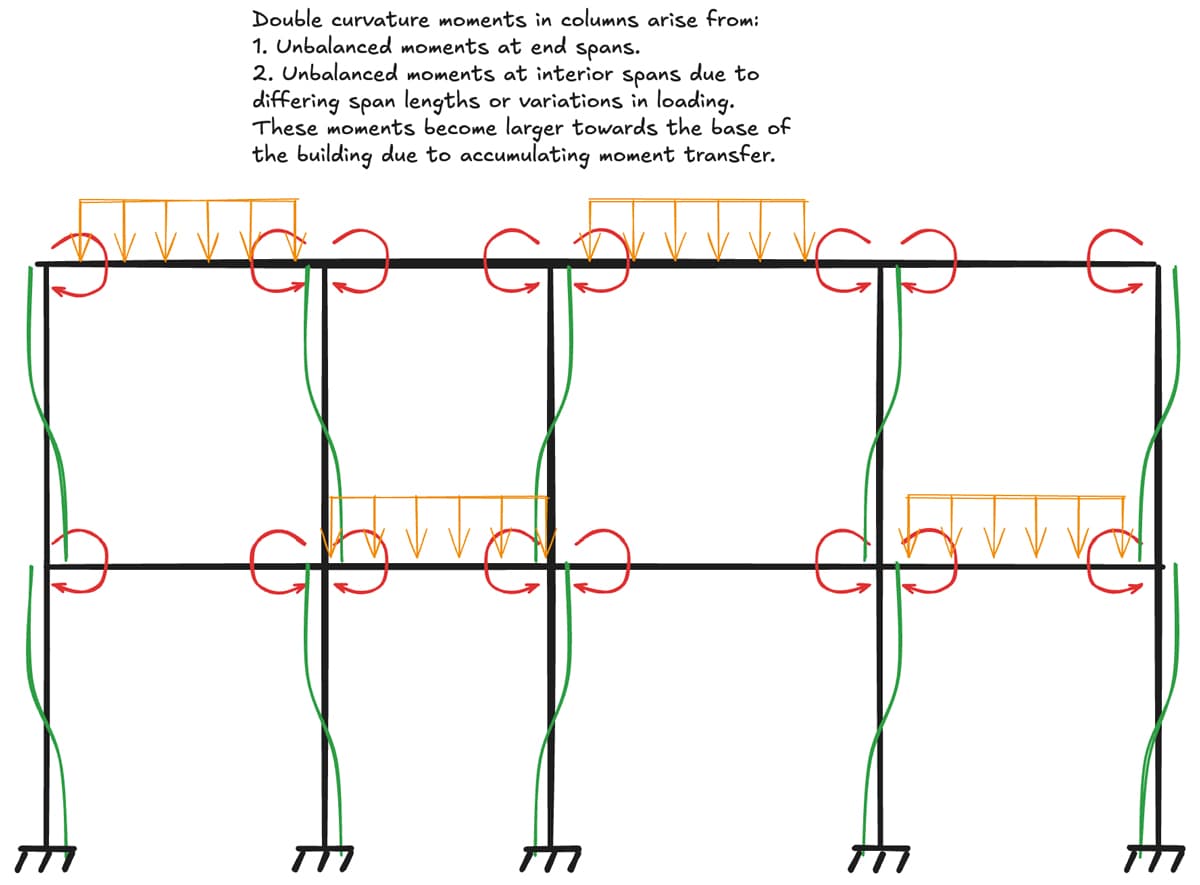
Figure 2: Typical moments induced by gravity loading.

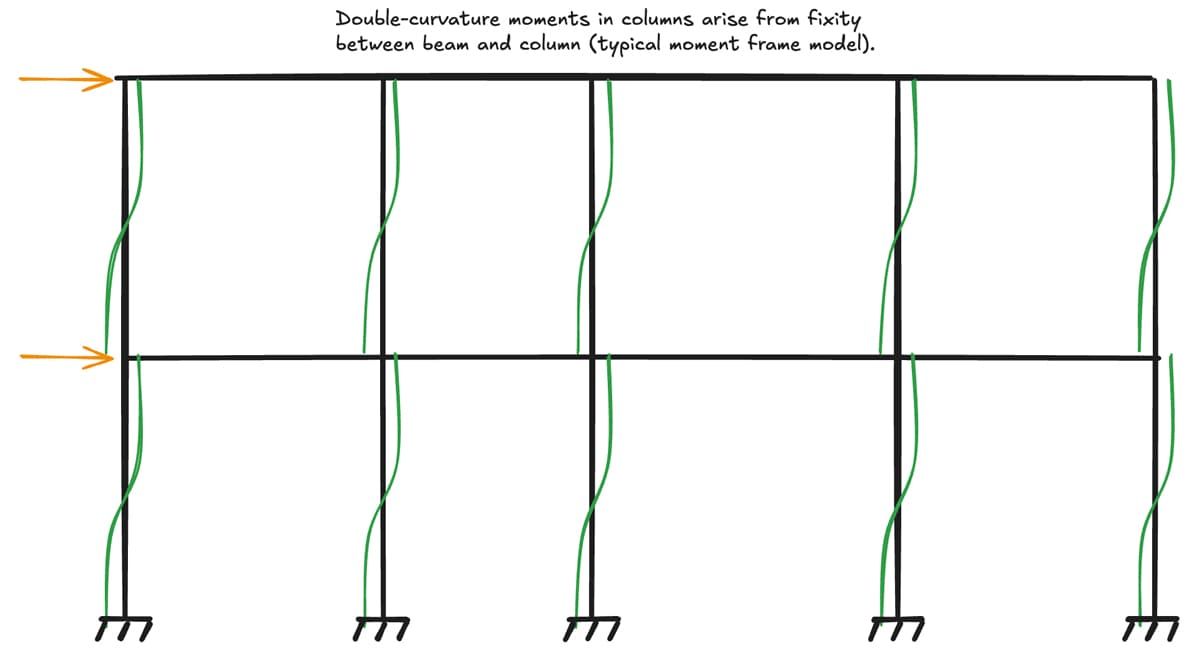
Figure 3: Typical moments induced by gravity loading.

As you can see, columns typically (though not always) bend in double curvature in addition to carrying axial loads. When viewed in this light, columns can, in the general case, be thought of as primarily axial load-carrying members and secondarily as flexural load-carrying members.

Having said all this, I should mention that it might be helpful to have read the previous tutorial on Concrete Beam Design using ACI 318-14 as there will be some overlap and continuation of concepts covered from there.

So, if a column resists both bending and axial loads, how do we analyse its capacity? Recall that failure can be said to have occurred in a concrete section when it reaches its ultimate crushing strain, $\epsilon_{cu} = 0.003$ (ACI 318-14 22.2.2.1).

Since both bending and axial loads contribute to compressive strains in the concrete, there must be some combination of each that will fail a column. Stated differently, on one extreme, a column could fail purely in bending (i.e. the classical beam).

On the other extreme, a column could fail purely axially (i.e. the classical column). Hence, one can infer that there should exist a possible permutation of both bending and axial loads that can cause a column to fail. In fact, there are an infinite! If there are an infinite ways that a column can fail, where do we begin to calculate our capacities?

2.0 Key analysis assumptions

Now that we've sufficiently motivated our discussion, let's start organising our thoughts and assumptions.

1. There exists some combination of moment and axial load that will cause our column to fail, i.e. moments and axial loads interact to bring the compressive concrete strain to $\epsilon_{cu} = 0.003$ at failure (ACI 318-14 22.2.2.1).

2. From mechanics of materials, we know the following to be true for any elastic beam element:

   $$\begin{aligned} \frac{P}{A} & + \frac{My}{I} = f_{cu} \\\\ \frac{P}{A f_{cu}} & + \frac{M y}{I f_{cu}} = 1 \\\\ \frac{P}{P_{max}} & + \frac{M}{M_{max}} = 1 \end{aligned}$$

3. Concrete is weak in tension. In fact, per ACI 318-14 22.2.2.2, tensile capacity of concrete cannot be taken into account in axial or flexural strength calculations. Thus, we will take the tensile capacity of concrete to be zero.

4. Reinforced concrete does not behave linearly. (Recall the concrete stress-strain curve!)

5. Strain-compatibility and equilibrium in the section must be met (ACI 318-14 22.2.1). Stated simply, this means that we assume the rebar and the concrete deform together and compression forces exactly equals tension forces under a given loading. For a vast majority of columns, this is a valid assumption. We shall assume a linear strain distribution in our concrete section - plane sections remain plane (ACI 318-14 22.2.1.2). This key assumption will form the basis of our calculations.

From our strain compatibility assumption, we are able to determine all the forces in our section by setting $\epsilon_{cu} = 0.003$ at one end and assuming a certain, arbitrary tensile strain at the other end. The below is a generic model:

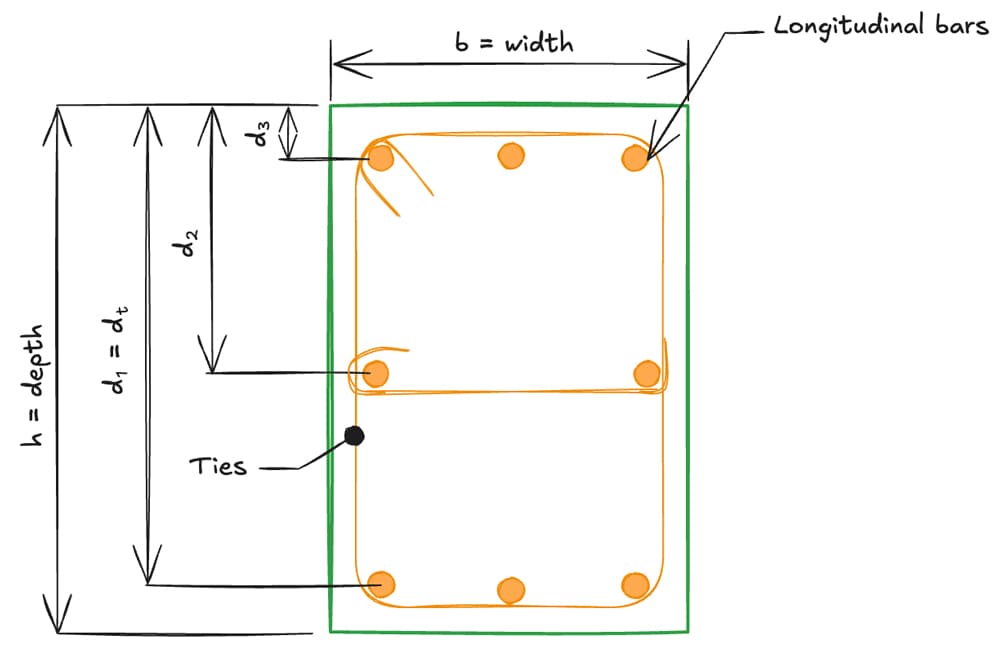
Figure 4: Typical column cross section.

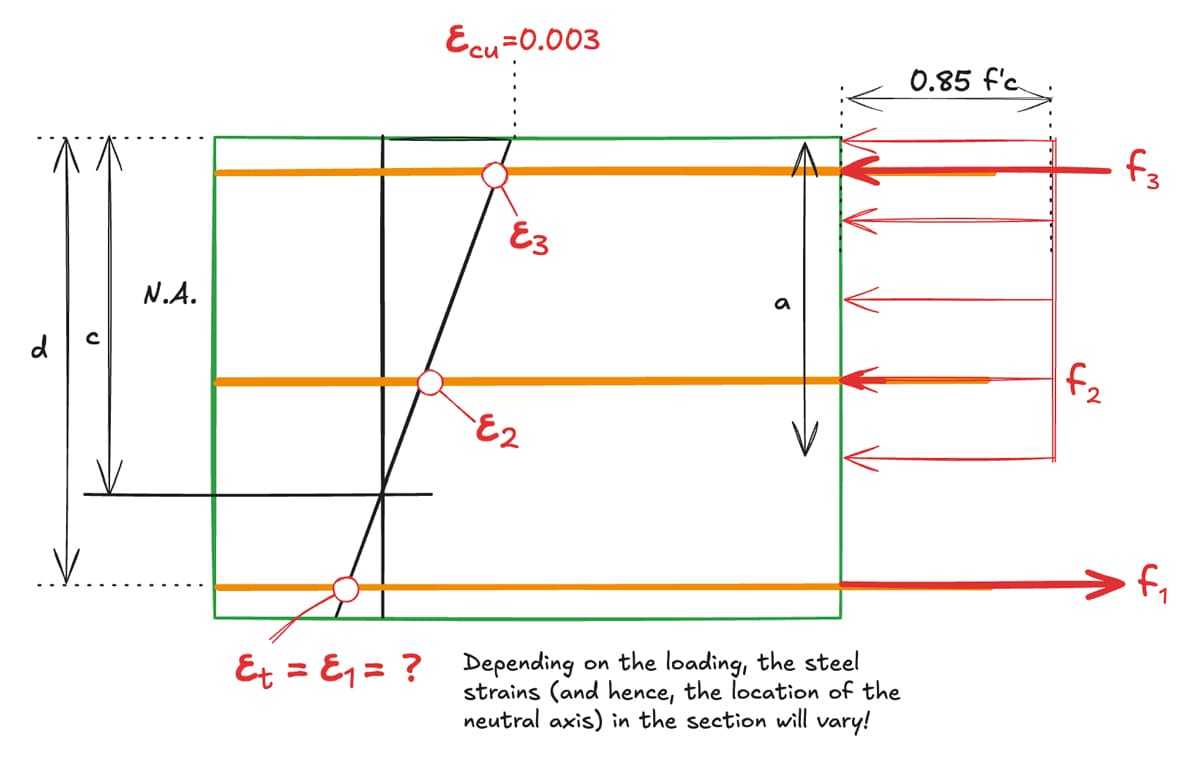
Figure 5: Linear strain distribution and equivalend rectangular stress block and force resultants.

Without doing any math, if we were to plot axial capacities on the y-axis (compression positive) and moment capacities on the x-axis, we can, from our above assumptions, infer that it might qualitatively look something like this:

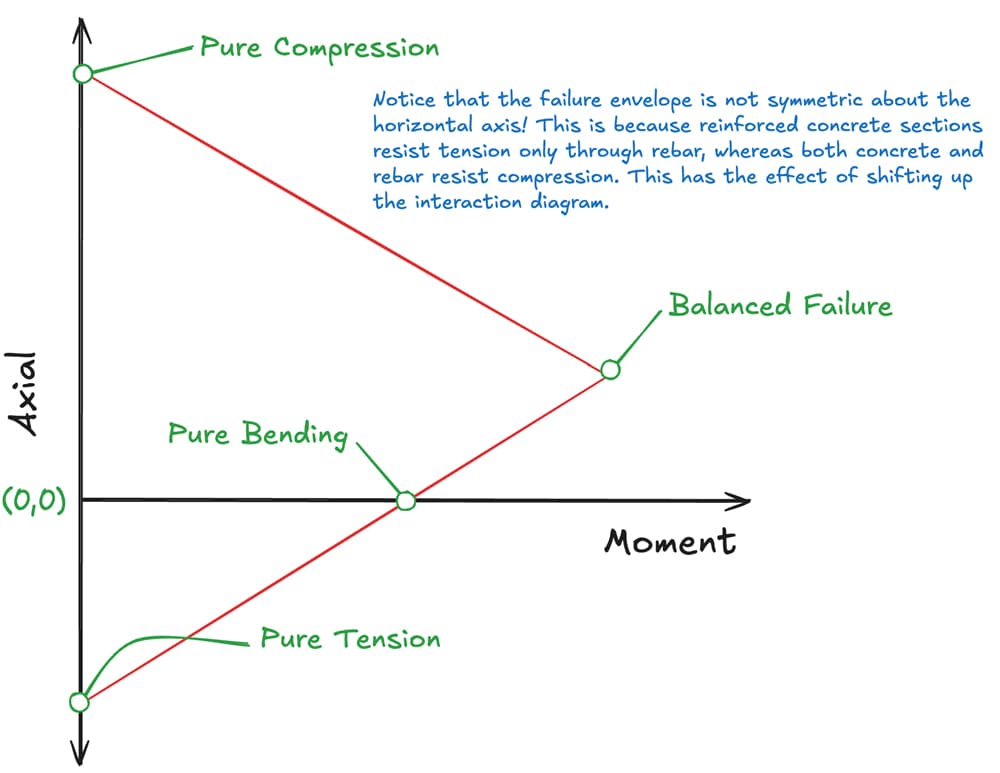
Figure 6: Qualitative plot of axial compression force capacity against moment capacity.

We are now able to find every point in our interaction diagram, but before we do so, let's dive into ACI 318-14 to help us understand which specific points may be of special interest to us.

3.0 Turning to ACI 318-14

Recall that for flexural and axial loads, ACI 318 specifies the strength reduction factor, $\phi$, based on the strain in the tension steel.